Несобственный интеграл 1 рода с бесконечным пределом. Несобственные интегралы. Несобственные интегралы от неограниченных функций

Рассмотрим два вида несобственных интервалов:

1. Несобственные интегралы I-го рода с бесконечными пределами интегрирования;
2. Несобственные интегралы II-го рода от функций с бесконечными разрывами.

Несобственные интегралы первого рода с бесконечными пределами интегрирования

Определение: Интегралы вида: называются несобственными интегралами I-го рода с бесконечными пределами, которые определяются с помощью пределов:

Определение Несобственные интегралы называются сходящимися, если существуют конечные пределы, с помощью которых эти интегралы определяются.

Несобственные интегралы называются расходящимися, если эти пределы не существуют или бесконечные.

Действительно, пусть функция f(x) определена и непрерывна при любом значении x=в из полубесконечного отрезка функций имеем:

Он сходится к 1. Тогда согласно теореме 1 несобственный интеграл от меньшей функции: также сходится и его значение меньше 1.

Теорема 2. Если для знакоположительных функций, для которых выполняется неравенство 0?g(x)?f(x), при любых х? а, несобственный интеграл от меньшей функции расходится, то расходится и несобственный интеграл от большей функции.

Пример. Исследовать сходимость интеграла:

Решение. Сравним подинтегральную функцию с функцией. Для знакоположительных на интервале , а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.

Геометрический смысл несобственного интеграла выясняется довольно просто. В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл выражает площадь криволинейной трапеции, ограниченной кривой y = f (x ) , осью абсцисс и ординатами x = a , x = b . В свою очередь несобственный интеграл выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x ) (на рисунке ниже - красного цвета), x = a и осью абсцисс.

Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:

Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.

Использование предела интеграла вместо самого несобственного интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то несобственный интеграл называется сходящимся, а в противном случае - расходящимся. К чему стремится переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода или второго рода. Узнаем об этом сейчас же.

Несобственные интегралы первого рода - с бесконечными пределами и их сходимость

Несобственные интегралы с бесконечным верхним пределом

Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.

Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.

Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.

Пример 1. Вычислить несобственный интеграл (если он сходится).

Решение. На основании определения несобственного интеграла находим

Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.

В следующем примере подынтегральная функция почти как в примере 1, только степень икса - не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?

Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).

Решение. Предположим сначала, что , тогда

В полученном выражении перейдём к пределу при :

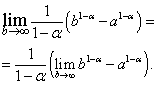
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .

В первом случае, то есть при имеет место . Если , то и не существует.

Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .

Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:

Это обобщённая формула Ньютона-Лейбница.

Пример 3. Вычислить несобственный интеграл (если он сходится).

Предел этого интеграла существует:

Второй интеграл, составляющий сумму, выражающую исходный интеграл:

Предел этого интеграла также существует:

Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:

Несобственные интегралы второго рода - от неограниченных функций и их сходимость

Пусть функция f (x ) задана на отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b , в то время как во всех остальных точках отрезка она непрерывна.

Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.

Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае - расходящимся.

Используя формулу Ньютона-Лейбница, выводим.

2 Несобственными интегралами первого рода называются интегралы вида Подынтегральная функция предполагается непрерывной на всем участке интегрирования.

2 Если существует и конечен предел , то говорят, что несобственный интеграл сходится и равен

Аналогично определяются интегралы и :

(8.21)
где а – любое действительное число. Причем про последний интеграл говорят, что он сходится тогда и только тогда, когда сходятся оба составляющих его интеграла.

Задача 8.10.

Решение.

Следовательно, интеграл расходится.

Задача 8.11. Вычислить несобственный интеграл .

Решение.

Данный интеграл сходится.

2 Несобственными интегралами второго рода называются интегралы вида: , где подынтегральная функция f (x ) имеет бесконечные разрывы на конечном отрезке [a ; b ]. Определяются несобственные интегралы второго рода по-разному, в зависимости от расположения точек разрыва на промежутке [a ; b ].

1) Предположим, что функция f (x ) имеет бесконечный разрыв в некоторой внутренней точке области интегрирования (c Î(a ; b )) В остальных точках отрезка [a ; b ] функция предполагается непрерывной.

Тогда, если существуют и конечны пределы и , то говорят, что интеграл сходится и равен

. (8.22)
2) Пусть единственная точка разрыва функции f (x ) совпадает с точкой а

. (8.23)
3) Пусть единственная точка разрыва функции f (x ) совпадает с точкой b . Тогда, если существует и конечен предел , то говорят, что интеграл сходится, и равен

. (8.24)
Всюду предполагается, что e > 0 и d > 0.

Задача 8.12. Вычислить несобственный интеграл .

Решение. x = 2. Следовательно,

Задача 8.13. Вычислить несобственный интеграл .

Решение. Подынтегральная функция имеет разрыв второго рода в точке x = 0 (внутри области интегрирования). Следовательно,

Первый предел существует и конечен, но второй предел равен бесконечности ( при ). Следовательно, данный интеграл расходится.

Глава 9. Функции нескольких переменных

§9.1. Определение n -мерного евклидова пространства R n .

Прежде чем перейти к изучению функций многих переменных полезно ввести понятие n -мерного пространства для любого n = 1, 2, 3,… .

2 Точкой x n -мерного пространства (вектором) называется упорядоченная совокупность n действительных чисел .

Число называется i -ой координатой вектора .

2 Расстояние между двумя точками n -мерного пространства и определяется по формуле:

Расстояние от точки до точки x называется модулем вектора x и обозначается . Из формулы (9.1) следует, что .

В n -мерном пространстве естественным образом вводится понятие скалярного произведения:

Угол между векторами x и y можно определить по формуле:

По прежнему, векторы x и y перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю.

2Совокупность всех точек n -мерного пространства, в котором определено расстояние согласно формуле (9.1) и скалярное произведение, называется n -мерным евклидовым векторным пространством и обозначается через .

В случае n = 1 пространство совпадает с прямой, в случае n = 2 – с плоскостью, а в случае n = 3 – с пространством.

2 Пусть и . Совокупность всех точек таких, что , называется n -мерным шаром с центром в точке x или e -окрестностью точки x в пространстве и обозначается .

В координатной форме это определение выглядит так:

В случае прямой, т.е. при n = 1, окрестность точки представляет из себя интервал с центром в точке радиуса e . В случае плоскости, т.е. при n = 2, окрестность точки представляет из себя открытый круг с центром в точке радиуса e . В случае пространства, т.е. при n = 3 окрестность точки представляет из себя открытый шар с центром в точке радиуса e .

§9.2. Область определения функции нескольких переменных. Непрерывность

2 Функцией n переменных называется такое правило (закон), по которому каждому набору, состоящему из n переменных , взятому из некоторой области D n -мерного пространства , ставится в соответствие единственное число z . В наиболее простом случае .

2 Функцией 2-х переменных называется такое правило (закон), по которому каждой точке M (x ; y ), принадлежащей некоторой области D плоскости xOy , ставится в соответствие единственное число z .

Множество точек в пространстве с координатами образуют некоторую поверхность (рис. 9.1), возвышающуюся над областью D (геометрический смысл функции двух переменных).

2 Область D , для которой построено указанное выше соответствие, называется областью определения функции .

Задача 9.1. Найти область определения функции

Решение. Искомая область определения является множеством точек на плоскости xOy , удовлетворяющих системе неравенств . Неравенства и меняют свой знак на противоположный (соответственно) при пересечении следующих линий: x = y и x = 0, y = 0. Эти линии разбивают плоскость xOy на 6 областей. Последовательно, подставляя произвольные точки, из каждой области в систему , убеждаемся в том, что объединение областей (1) и (3) является областью определения исходной функции. Причем прямая x = y , за исключением точки (0; 0), входит в область определения, а прямые x = 0, и y = 0 – не входят (рис. 9.2).

2 Замыканием области называется множество точек пространства , в любой окрестности каждой из которых содержатся точки области D .

Пусть, например, D – некоторая открытая (граница не включается) область на плоскости xOy . Тогда замыкание области получится, если к области D присоединить ее границу Г .

2 Пусть в некоторой области D плоскости xOy задана функция , и пусть – некоторая точка замыкания области D (). Число А называется пределом функции в точке М 0 , если для любого числа e > 0 найдется такое число δ > 0, что для всех точек , отличных от точки М 0 и удаленных от нее меньше, чем на δ , выполнено неравенство .

2 Функция называется непрерывной в точке если она определена в этой точке () и имеет место равенство .

§9.3. Линии уровня функции двух переменных

2 Линии на плоскости xOy , заданные уравнениями , где С – произвольная константа, называются линиями уровня функции .

Линии уровня являются линиями пересечения поверхности, заданной функцией и плоскости z = C , параллельной плоскости xOy . С помощью линий уровня можно изучать форму поверхности, заданной функцией .

Пример 9.2. Найти линии уровня и определить форму поверхности, заданной уравнением .

Уравнения линий уровня в данном случае имеют вид . При C < 0 уравнение дает пустое множество решений (следовательно, вся поверхность расположена выше плоскости xOy ). При C = 0 уравнению линии уровня удовлетворяет только одна точка x = 0, y = 0 (с плоскостью xOy поверхность пересекается только вначале координат). При C > 0 линии уровня являются эллипсами , с полуосями и . Линии уровня, соответствующие различным значениям С , изображены на рис. 9.3. Поверхность, заданная уравнением , называется эллиптическим параболоидом (рис. 9.4).

§9.4. Частные производные первого порядка

Пусть в некоторой области D плоскости xOy задана функция , и – некоторая точка области D .

, (9.2)

2 Частной производной функции в точке по переменной y (обозначается или ) называется

, (9.3)
если данный предел существует и конечен.

2 Частной производной функции n переменных в точке по переменной x i называется

, (9.4)
если данный предел существует и конечен.

Как видно из формул (9.2) – (9.4), частные производные определяются аналогично тому, как определялась производная функции одной переменной. При вычислении предела приращение получает только одна из переменных, остальные переменные приращения не получают и остаются постоянными. Следовательно, частные производные можно вычислять по тем же правилам, что и обычные производные, обращаясь со всеми свободными переменными (кроме той, по которой производится дифференцирование) как с константами.

Задача 9.3. Найти частные производные функции

Решение. .

Задача 9.4. Найти частные производные функции .

Решение. При дифференцировании данной функции по переменной x мы пользуемся правилом дифференцирования степенной функции, а при нахождении частной производной по переменной y – правилом дифференцирования показательной функции:

Задача 9.5. Вычислить частные производные функции в точке .

Решение. Применяя правило дифференцирования сложной функции, найдем частные производные

Подставляя в частные производные координаты точки М , получим

§9.5. Градиент функции нескольких переменных.
Производная по направлению

2 Градиентом функции в точке называется вектор, составленный из частных производных данной функции, вычисленных в данной точке:

2 Производной функции в точке по направлению вектора называется проекция вектора градиента данной функции, вычисленного в точке М 0 , на данное направление

Вычисляя проекцию вектора на вектор в соответствие с формулой (2.6), получим

. (9.7)
Замечая, что , где a – угол, который вектор образует с осью OX , получим еще одну формулу для вычисления производной по направлению вектора

Задача 9.6. Найти градиент функции в точке М 0 (4; 2) и производную по направлению вектора

Решение. Найдем частные производные

Вычислим значения частных производных в точке М 0:

Градиент функции в точке М 0 найдем по формуле (9.5):

Задача 9.7. В точке М 0 (0; 1) вычислить производную функции по направлению биссектрисы второго координатного угла.

Решение. Найдем частные производные функции :

Вычислим значения частных производных и градиент функции в точке М 0:

Производную функции в точке М 0 по направлению биссектрисы второго координатного угла (данное направление составляет с осью OX угол a = 135°) найдем по формуле (9.8):

§9.6. Дифференциал функции нескольких переменных
и его применение к приближенным вычислениям

1 Если в точке функция имеет непрерывные частные производные и , то ее полное приращение при переходе от точки М 0 к точке может быть представлено в виде:

, (9.9)
где при , .

2 Выражение называется полным дифференциалом функции в точке .

Из формулы (9.9) следует, что дифференциал функции является главной линейной частью полного приращения функции . При достаточно млых Dx и Dy выражение существенно меньше дифференциала и им можно пренебречь. Таким образом, мы приходим к следующей приближенной формуле:

. (9.10)
Замечание. Формулой (9.10) можно пользоваться для приближенного вычисления значений функций только в точках , достаточно близких к точке . Чем меньше значение , тем точнее значение , найденное по формуле (9.9).

Пример 9.8. Вычислить приближенно, с помощью дифференциала.

Рассмотрим функцию . Требуется вычислить значение z 1 этой функции в точке (x 1 ; y 1) = (0,09; 6,95). Воспользуемся приближенной формулой (9.9), выбрав в качестве точки точку (0; 7). Тогда Dx = x 1 – x 0 = 0,09 – 0 = 0,09, Dy = y 1 – y 0 = 6,95 – 7 = – 0,05.

Следовательно,

§9.7. Частные производные высших порядков

Пусть в области D задана функция , имеющая в этой области непрерывные частные производные и . Таким образом, в области D мы получили две новые непрерывные функции двух переменных и . Если в некоторой точке области D функции и имеют частные производные как по переменной x , так и по переменой y , то эти производные называются производными второго порядка функции . Они обозначаются следующим образом:

1 Если в некоторой точке области D функция имеет непрерывные смешанные производные и , то в точке эти производные равны: . D , необходимо выполнение условий: D = 32 – 9 = 23.

Так как дискриминант больше нуля, то в точке М функция имеет экстремум. А именно, локальный минимум, поскольку А и С больше нуля. При этом